How they tuned the guitar download this page as a pdf

The guitar has a very long history; it has evolved over the ages to what it is now. It has achieved its final distinct form in 1770, at which time it became the instrument we recognize today with 6 strings and frets on an elongated neck with tuning keys at one end and a large resonating body at the other. The immediate ancestor of the guitar had 5 strings and I imagine that they used the tuning ideas they developed for the 5 string guitar to tune the 6 string. However, I am not going to go down that road because that would lead to another ancestor with 4 strings, etc. I am going to try to imagine how someone would have developed a tuning system from scratch for a 6 string guitar and see what knowledge can be gleaned from that.

The basic principle of making a 3-note chord is to start with the tonic of a scale and skip every subsequent note in that scale. The same chord that you make on a piano you can make on a guitar. However a guitar is not like a piano where every note is laid out in a linear pattern. The guitar is like a series of 5 keyboards each one with its own layout. It is more complex than the piano because it is compact; the piano has a string for every one of its 88 notes, the guitar has only 6 strings. The guitar can sound 47 notes with 21 frets but it doesn't have 47 strings, and that's why the complexity. Instead of having one string per note the guitar has 6 notes per fret, providing many notes into a short space. But it's not sufficient to have 47 notes in a short space; one must be able to make those beautiful sounding chords that a piano makes.

Each string when plucked its full length needs to be tuned to a specific note. The goal is to make chords as easy as possible to play with 4 fingers and the guitar must be tuned (a different note to each open string) such that the finger positions are easily positioned on the appropriate fret. The genius of the early guitar makers was to come up with a tuning system that provided 5 basic chord shapes and their derivatives (minor, major, augmented, etc) that could be comfortably played. Those five basic chord shapes are the C, A, G, E and D shapes that are known collectively as the CAGED chords.

In the diagrams that follow, the thick line represents the nut which fixes the length of the string between it and the bridge. A struck open string is the lowest note on that string.



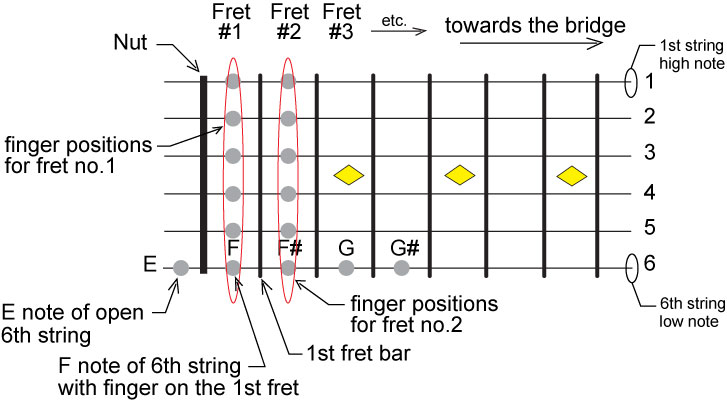
How did the early guitar makers come up with the tuning or specific note for each guitar string? What was the thinking that led them to the pattern of chords that we know today? I suspect they used trial and error and focused their efforts on making them as compact as possible. Perhaps also the technology of the times limited the range of the notes that the strings could play for a certain frequency range, but this is speculation. As a starting point, I will assume that for whatever reason they decided that E would be the lowest note on the guitar, the open 6th string.



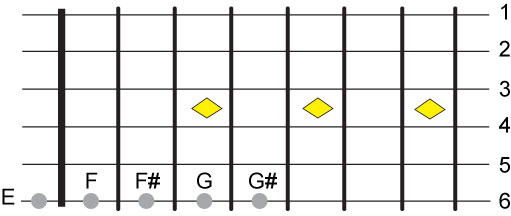
Let's reverse engineer the guitar and along the way discover the mysteries of its construction which will help us play, understand the guitar and be better musicians.

Each note on a string is separated by a fret which provides a semi-tone or a fret-step interval. Every note in Western music can be produced over a range of several octaves.

Let's start by positioning the C major chord, seems like a reasonable starting point, everyone learns the C major scale first and C is its first chord. The notes of C major are C-E-G. This is independent of the instrument and is dictated by music theory. Since the 6th string is an E, the 5th string will have to contain the C, the first note of C major chord somewhere on the fretboard, the question is which fret. The 5th open string has to be higher than E since there is not much point in making it the same note. Let's assume that the 5th open string is between G# and B. Why start with G#? It seems logical to try to keep all the notes of a chord within a short span such as the first 3 frets. Three frets down from the note E of the open 6th string brings us to a G, then G# is a good starting point for the 5th string. The C can lie anywhere between the 1st and the 4th fret. You can see that if the 5th string is tuned to B, C can be on the 1st fret, if it is tuned to Bflat, C can be on the 2nd fret and if it is tuned to A, C can only be on the 3rd fret, etc.



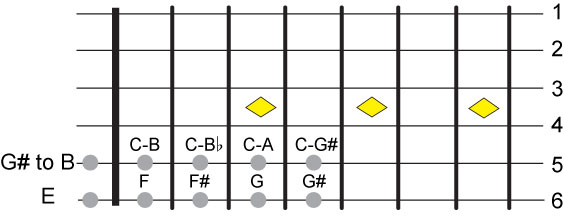
If we want to keep the C chord notes within the first 3 frets the range of the 5th open string should be A to B.



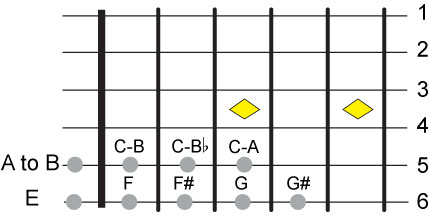
The C major chord has these 3 notes C-E-G. So the 2nd note can either be an E or a G.

Why is the 2nd note either an E or a G? On the piano, the notes of chords are typically played simultaneously. You can pluck 3 guitar notes at the same time but they are often strummed and when they are strummed you should always start with the root of the chord in this case C, this establishes the predominance of the lowest note, you can then play either the 2nd and 3rd note in that sequence or in reverse sequence, the ear cannot tell the difference.

If we try to position the G on the 4th string, G is a lower than A or B on the 5th string and therefore cannot belong to that string, therefore the second note has to be the E on that string. The E can be anywhere on the 4th string between the 1st and 3rd fret if the 4th string open note is between C# and D#.



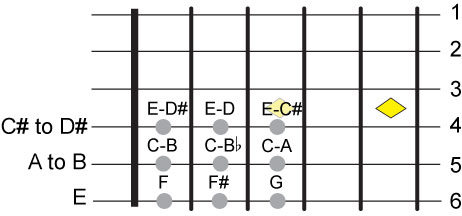
The A major chord has the notes A, C# and E and the A has to be somewhere on the 5th string. Looking at the 5th string we see that B can be the open string note, if we chose B as the open note then all subsequent notes have to be higher than B which eliminates the possibility of A being on those frets. Therefore A has to be on that string and it must be the lowest note or the open string note.



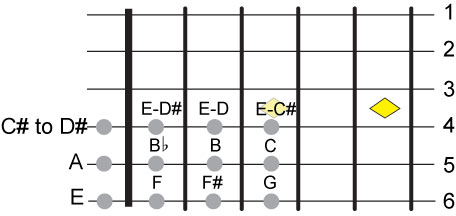
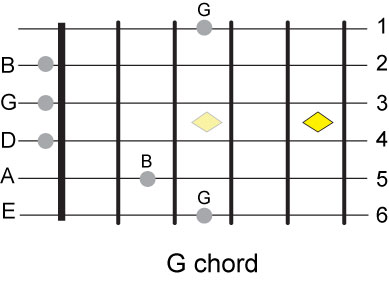
The G major chord has the notes G, B and D. We have a G on the 6th string 3rd fret, then a B on the 5th string 2nd fret. The 3rd note can only be a G or a D, the G is not possible on the 4th string therefore it must be a D. Since we need an E somewhere on that string the only way to have both an E and a D is to have the D on the open string or on the 1st fret.

Let's take another tack and see if we can create an easy relationship between the open notes of the 6th, 5th and 4th strings. On the 6th string because E is the open note, A will be the 5th fret note. A is also the open string note of the 5th string, if we use that same pattern for the 4th string then D will be the open note of the 4th string. This is a way of resolving the question discussed above of where the D note is on the 4th string.



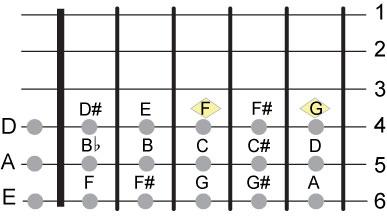
If we follow the same pattern between the 4th and the 3rd string, the 3rd string open note will be a G.



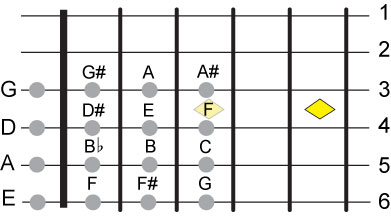
Let's apply the same relationship between the 3rd and 2nd string. The open note of the 2nd string is then a C.

At this point we have all the notes down to the 2nd string and arrived there without trying to fit too many complete chords so we are not sure what the resulting chord shapes will be like yet but it seems advantageous to have these note relationships between strings, it will make it easy to identify notes on the frets. We will just have to wait and see where the notes fall on the fretboard that make up the chords and determine if it is practical.



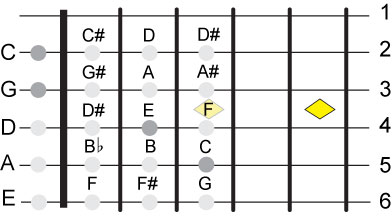
Let's examine the C chord (C-E-G), the first 3 notes in the sequence is C-E-G on strings 5, 4 and 3 respectively. This is a complete chord since it has 3 different notes however we can use more notes as long as they are C, E or G to create a more harmonious chord.

The 4th note can only be a C or an E, there is an E on the 2nd string of the 4th fret but this is outside the range of 3 frets that we have given ourselves so E cannot be the 4th note. C must be the 4th note and one way to attain this is to make the 2nd open string a C.



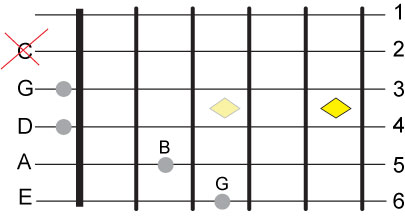
Let's see how the G chord fits this arrangement. The G chord is made up of G, B and D. The full sequence of notes will be G, B, D, G, B and D.

It is required that the 5th note which is on the 2nd string be a B but this is not possible because of the way we have positioned the C note. Therefore the C note will have to be moved up one fret to accommodate the B on the 2nd string for the G chord.



This makes the C chord look like this:



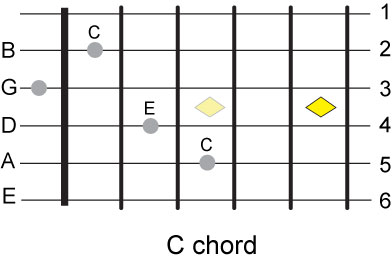
This breaks the pattern that we established between the strings allowing easy identification of notes from one string to another but there was no choice since we could not have played the G chord.

To determine the open note of the 1st string we carry on the same relationship between 6, 5, 4, and 3rd strings that is we make the open note of the 1st string an E the same as the 5th fret note of the 2nd string.



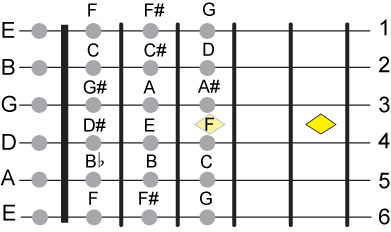
Having established all the notes for the first 3 frets on all 6 strings let's see if we can play all the major chords within this range making sure the position of the fingers is practical. This is important since finger positions will get more complicated as one extends the range of chords played to variations such as minor chords , 7th or 11th, etc.

We have shown what the C and G chords looks like; here are the rest of the major chords.







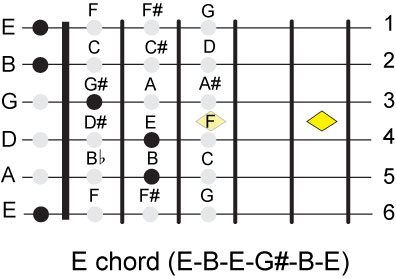
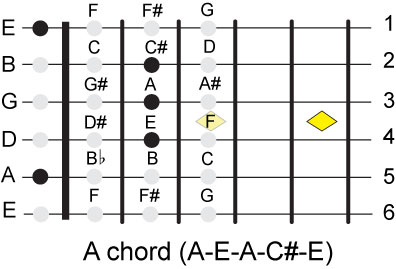
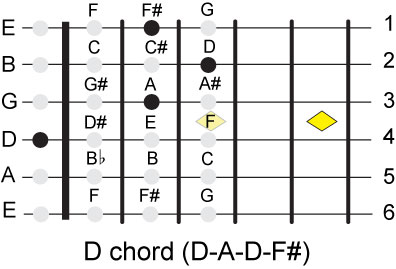
This is a good point to recap what we have done and list all the assumptions that we used, these are the principles of the standard guitar tuning.

1. The 6th open string note is the E and is the lowest note of the guitar;

2. The root of a chord is always played first and is the lowest note of the chord;

3. Chord notes are consecutive (no strings are skipped) at least for major and minor chords, two consecutive notes cannot be identical and the sequence of notes does not have to follow the music theory sequence;

4. Each open string note is 5 fret-steps higher than its predecessor, except the 2nd string is 4 fret-steps higher than the 3rd string.

We are missing 2 chords from the complete set of major chords looked at so far and these are F and B.

F is one fret-step higher than E so that the first note of the F chord is on the 6th string 1st fret. If every note of the E chord is moved up one fret-step we get the F chord.



Many notes are required to sound the F chord and not enough fingers to play them. This is solved by using the index finger to pay all the notes on the 1st fret which acts like a bar so the F chord when played this way is called a bar chord. A bar chord is typically shown like this:



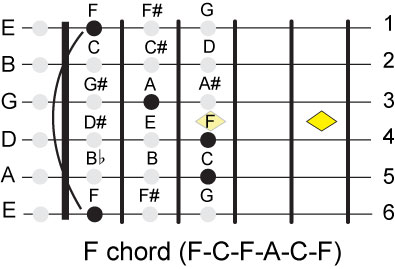
The curve line indicates that all the notes that are bracketed are covered by one finger leaving the 3 other fingers to play the remaining notes.

We can move this bar chord all the way down the neck to produce at least 11 successive chords (F#, G, G#, A, Bflat, C, C#, D, D#, E, F) depending on the length of the neck.

The other chord is the B and it can be constructed by moving up every note of the A chord by 2 fret-steps.



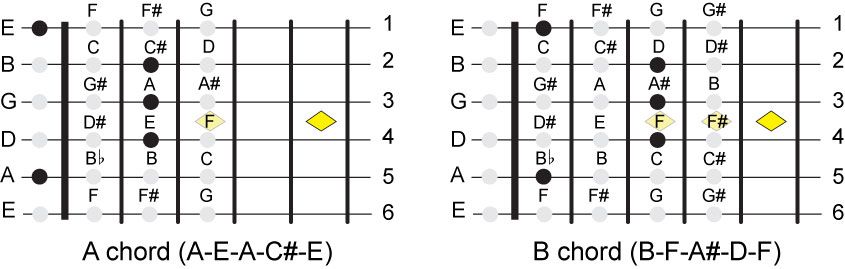
The B is also played as a bar chord.



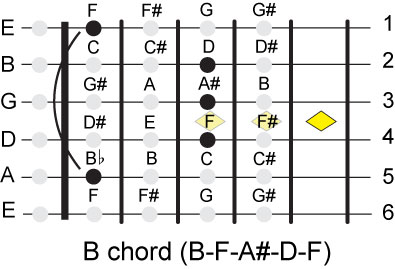
Here also we can move this bar chord all the way down the neck to produce at least 11 successive chords (C, C#, D, D#, E, F, F#, G, G#, A, Bflat and C) or more.

And the same is true of the C, D and the G, these forms can all be moved upwards as a bar chord. This has become known as the CAGED chords because the 5 chord shapes can be duplicated all down the neck giving you access too many chords in the whole range of frequencies available to the guitar.

Up to now we established how major chords can be played on the first 3 frets of the guitar but what about minor chords? Most songs are not played with major chords only but they are a combination of major and minor chords. Very often a song is played in a recognizable key, the key is the root or tonic of a scale and very often the major scale is used because it is very familiar to our ear. The chords of the C major scale are: C, Dm, Em, F, G, Am and Bdim. For more information about how chords are formed from a major scale see: http://www.chordsandguitar.com/distillation.htm .

Let's look at all the major chords we have shown up to now and show how their minor version will be played. A major chord is comprised of the tonic of a major scale, using the C major scale we start at C, skip the D, keep the E, skip the F and keep the G or C-E-G. The notes of the scale can be numbered: 1, 2, 3, 4, 5, 6, 7. The pattern is then 1-3-5 for the first major chord of that scale. To make the minor version of that chord we flatten the 2nd note, so that we get 1-flat3-5. 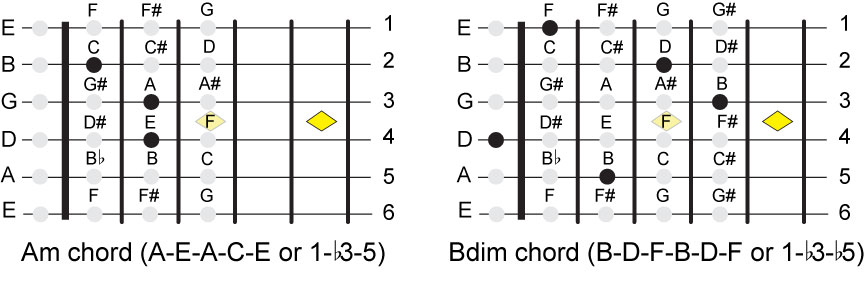Let's see what the Dm, Em, Am, Bdim look like based on the standard tuning. The Bdim chord has a flat 3 and a flat 5 so its code is: 1-flat3-flat5. This matches up with the chords of the C major scale shown above.





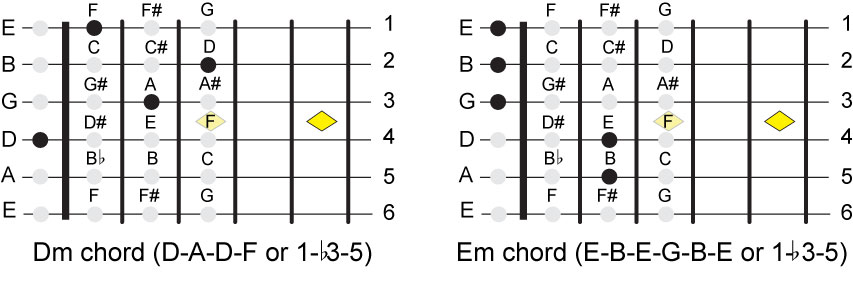
And to be complete we will show the Fm and Gm chords.



This I believe is how the standard guitar tuning was achieved. It's speculation but I think not too far-fetched.